An accelerometer was mounted on a disc, with a piece of paper connected to it. The accelerometer was used to measure the acceleration in the x and y direction and the piece of paper was used to pass through a photogate so that the period of rotation of the spinning wheel was recorded.
Measurements Made:
1. Length of time for a period to make a couple rotations
2. The accelerometer reading the rotational speed
3. Distance of the accelerometer from the center of the rotating disk
acceleration = radius * rotational speed^2 (a=rw^2)
radius = 13.8-14 cm
Procedure:
1. We gave the motor connected to the disk some voltage and recorded the acceleration. We then recorded the period of time using Loggerpro's photogate and the piece of paper sticking out from the edge.
2. We then received a graph of the acceleration and a data table for the period.
Each Trial:
1. 4.4 voltage on the motor:
 |
| Acceleration: 1.557m/s^2 (mean) |
 |
| Time: (8 rotations-start time)/8 = (16.461-1.672)/8 = period in seconds |
2. 6.4 voltage on the motor:
 |
| Acceleration: 5.074 m/s^2 |
 |
| Time: (10 rotations-start time)/10 = (10.5305-0.1789)/10 = period in seconds |
3. 9.6 voltage on the motor:
 |
| Acceleration: 11.89 m/s^2 |
 |
| Time: (10 rotations-start time)/10 = (6.784-0.0534)/10 = period in seconds |
4. 10.8 voltage on the motor:
 |
| Acceleration: 18.15 m/s^2 |
 |
| Time: (10 rotations-start time)/10 = (5.865-0.377)/10 = period in seconds |
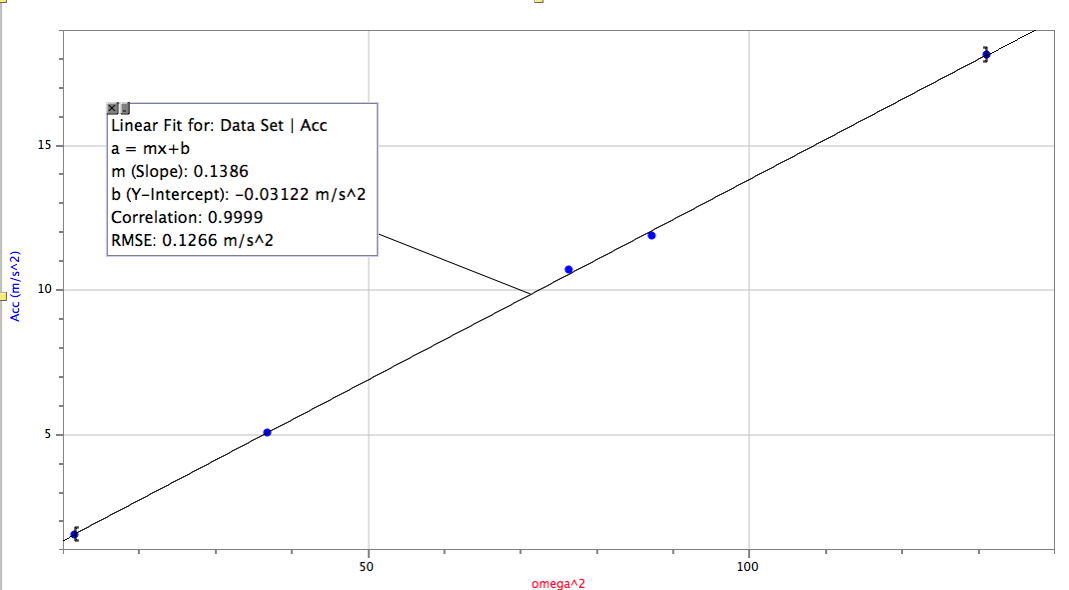
We then plotted and acceleration vs w^2 graph. Acceleration was found using the mean of the data graphs and the omega was found by w=[2(pie)]/T where T was the period that we found.
After creating a linear fit with our data, we proved that the relationship between acceleration and omega^2 is r since the radius of the disc was 13.8-14 cm and the slope was 0.1386 (meters).


No comments:
Post a Comment